Genomic Data Commons
学生時代、その解析に躍起になっていたThe Cancer Genome Atlas Networkのデータが全て新しいプラットフォームである
Genomic Data Commons Home | NCI Genomic Data Commons
へ移行した。あれこれやってみて使い方が見えてきたので備忘録として残しておく。
まずデータのダウンロード。ぼくはRNA-seqのデータを使います。今回のデータベース移行は、よくよく考えてみれば合理的で、各症例のシークエンスデータが一つのファイルとしてまとめられている。これを非常にわかりやすいブラウザ上のユーザーインターフェイスを使って使いたいデータを選ぶ。
ぼくは乳がんのRNA-seqで自由に使えるデータ、3,666症例のシークエンスデータをダウンロードしました。それぞれ、FPKMで格納されています。ダウンロードは一つ一つ手作業で3,666はさすがにヤバイので、専用のコマンドが用意されています。
gdc-client
という実行ファイル。Windows, Mac OSX, Linux対応。
./gdc-client download -m [manifest]
を実行。ここの[manifest]はポータルサイトで症例を指定すると自動で作成されるテキストファイルです。実行を開始すると延々とダウンロードが開始されます。ホームディレクトリでやると死亡するので注意しましょう。
今回は大きな一つのデータフレームではまとめてくれていません。一症例につき一つのディレクトリです。マジか。これを処理するために一つpythonでプログラム書かなきゃだめか。
内容は単純で、遺伝子のensenbl IDとFPKMの二行。なるほど、これなら新しい症例が増えるたびにデータフレームを編集しなくても良い。合理的ではありますね。
みどり本攻略 Day2
この記事は後でリライトすることを前提として得た知識をとりあえず書きなぐっています.わかりづらいことはご容赦ください.
----
さて,今日は一般化線形モデル generalized linear modelについて.みどり本の3章を読んでいきたいと思います. 前回の記事では,どの個体でも平均種子数が変化しないという前提でモデリングを行いました.今回,みどり本では植物の大きさと肥料を使ったか使わなかったかという二つの説明変数が加わった状態でモデリングを行います.
今回は,あまりRのコードには触れず,自分なりのここまでのまとめをメモしていきたいと思います.
まず統計モデリングを使う意義:私たちは自然現象を観測して,そこから法則を見出そうとしている.私の過去の研究から言えば,ある遺伝子の発現量が患者の予後に関わっている.ということを明らかにしようとすることもその一つだ.実際に観測したデータ(ex.遺伝子発現量と予後のデータ)について,その裏側に隠された自然界の法則(統計モデル)に似たような統計モデルを作る,ということを行う.
ある遺伝子の発現量がどれくらいであれば,予想される予後はどれくらいかという統計モデルを作ることになる.
さて説明変数によってパラメータが変化するとき,この統計モデルを観測データに当てはめることを,今回はポアソン分布に従うと仮定しているので,ポアソン回帰 Poisson Regressionと呼ぶ.そしてこのような統計モデルを一般化線形モデル generalized linear model,GLMと呼ぶ.
前回学んだように離散的な数値を取り最小がゼロであることはわかっているものの,最大はわからない場合にポアソン分布をとりあえず使う.
GLMでは重要な概念として線形予測子 linear predictorとリンク関数 linc functionがあり,これは(リンク関数)=(線形予測子)という関係性である.
ポアソン回帰の場合は,対数リンク関数を使用する(ことが都合が良い). ポアソン分布では0より小さい値を取り得ないため,対数であることは都合が良い.
λi = exp(β1+β2*xi)
log λi = β1+β2*xi
みどり本攻略 Day1 あとがき
みどり本ではある個体からできる種子の数を題材として進めているので,Wikipediaにも記載のあった1時間あたりに特定の交差点を通過する自動車の数という題材で記事を書いてみるのは,わかりやすいかもしれない.そうすると,データの数は24時間分で済むのかなと思ったり. それとも30日分のデータとして,週末や交通規制,天気といった情報を入れてみるのも面白いのかもしれないです.そうすればGLMにつながっていくかもしれない.
みどり本攻略 Day1
Rの復習と統計の勉強を兼ねて.みどり本とは「データ解析のための統計モデリング入門」という素晴らしい本です.学部時代にざっと読んだのですが,結局字面を追うだけでよく理解していなかったのでこの際再度しっかり学ぶことにしました.1日1章くらいのペースで読んでいければいいなと思います.基本的には自分のノートとして記述しますが,間違いなどあれば指摘していただけると幸いです.
この本の読者として想定しているのは...「数理モデルで現象を表現・説明する」基礎訓練を受けていない人たちです.
(まえがき より)
まさしく私のことです.
人は自然現象を観測しますが,その観測の数や程度は限られています.だから観測データをもとにその裏に隠された自然現象の法則(まさしく神さまのデザイン)を明らかにするために統計モデルを作って普遍化することが必要なのかなと思います.医学の世界では結構適当な統計もどきで有意差が出て大喜びということがありうるので,自らを律する意味でもしっかり学びたいと思います.
***
さて,初日の今日は2章を読みます.もちろんそのままコピーするのは良くないので,自分なりに学んだポイントを挙げていきます.
みどり本ではある植物の種子の数をもとに統計モデルを作るという題材で,解説していますが,最初のサンプルデータを変えて挑戦してみます.ある植物50個体の種子の数の架空データを使用しますが,あえて100個体分のデータを作って同じようにやってみます.
ネタバレ感がありますが,最初にデータを生成します.
data <- rpois(100, lambda=4.5)
これで data にポアソン分布に従う平均4.5の擬似乱数が100個格納されました.
このdataについてRの関数を使用して,さまざまな統計量を調べていきます.
summary(data)
Rはsummary()で色々出してくれるのがありがたいですね.
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 3.00 5.00 4.77 6.00 14.00
次に平均値を出してみます.
mean(data)
[1] 4.77
今回のデータは平均値が4.77です.
標本統計量も出してみます.
標本分散 sample variance
var(data)
[1] 5.512222
標本分散は,標本の相加平均をそれぞれの標本から引いて二乗した値の相加平均.
その平方根が標本標準偏差 sample standard deviation
sd(data)
sqrt(var(data)) #sqrt()は平方根を計算する
[1] 2.347812
さてここまででわかった今回のデータn=100について
平均値(相加平均):4.77
中央値:5.00
最大値:14.00
最小値:0.00
25パーセンタイル値:3.00
75パーセンタイル値:6.00
標本分散:5.512222
標本標準偏差:2.347812
以上のことがわかりました.
次にこのデータを統計モデルに当てはめていきます.
さてみどり本の記述では
統計学における推定.自然を確率分布であると見立てて,得られたデータをそこから発生した乱数のセットだと考える.限定された個数のデータから元の確率分布に近い確率分布を探すのが「推定」
とあります.今回のデータを「自然」としてこれを確率分布であると見立てます.
さて確率分布 probability distributionとは確率変数 random variableの値と出現する確率を対応させたもの,です.確率分布にはいろいろなものがあり,それぞれにパラメータが設定されています.ここではポアソン分布を使用します.確率変数はここで言うところのある個体の種子数といったそれぞれにばらつく値です.
ポアソン分布 Poisson distribution
所与の時間間隔で発生する離散的な事象を数える特定の確率変数 X を持つ離散確率分布のことである。(Wikipediaより)
意味がわからないので、具体的な例を挙げると
ということがあるようです.
ポアソン分布を用いる状況は,
(1) データが正の整数と0である. 離散的.
(2) 下限はわかっているが上限はわからない.
(3) データの平均と分散が大体等しい.
今回のでデータは平均が4.77なので平均4.77のポアソン分布をグラフとして図示してみようと思います.この流れ自体はみどり本に詳しい記載があります.
y <- 0:14
prob <- dpois(y, lambda = 4.77)
これでprobには種子の数が0個から14個それぞれの場合の平均4.77のポアソン分布に従う確率が格納されます.
prob
[1] 0.0084803802 0.0404514134 0.0964766209 0.1533978272 0.1829269089
[6] 0.1745122711 0.1387372555 0.0945395298 0.0563691947 0.0298756732
[11] 0.0142506961 0.0061796200 0.0024563990 0.0009013095 0.0003070890
こんな感じです.さて図示してみます.
plot(y, prob, type="b", lty=2) #"b"は丸と折れ線,2は折れ線を破線にする
できた図はこれです.
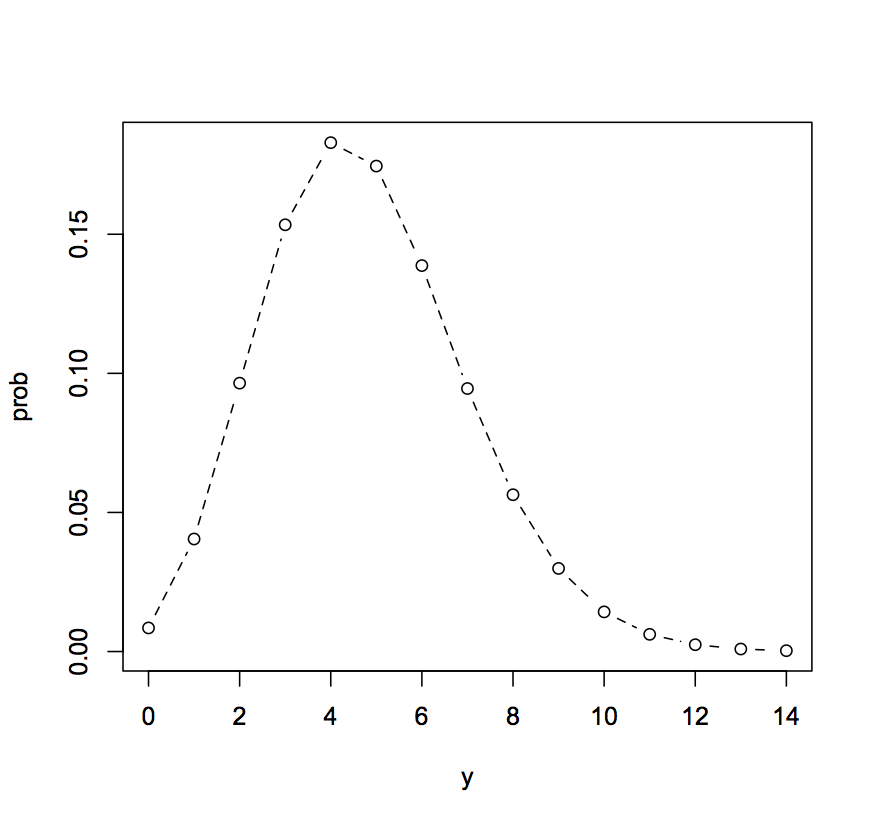
これを見ると一番出現確率が高そうなのは4でしょうか.
では確率分布のパラメータを観測データに基づいて推定する方法として最尤推定を考えます.尤度の概念はすごくわかりやすい解説を発見したので下記に記します.
こちらを発見.
尤度関数の基本概念は、「サンプリングしてデータが観測された後、そのデータは元々どういうパラメーターを持つ確率分布から生まれたものだったか?」と言う問いに答えるためのものです。
その後も非常にわかりやすい解説が並びます.勉強になりました.
とりあえず尤度自体は扱いづらい数(すごく小さくなって小数点以下が長くなる)なので,対数変換して対数尤度関数 log likelihood function を使います.
尤度は実際のところ,それぞれの確率変数が出現する確率の積です.
さて,みどり本に従ってRを動かします.
logL <- function(m) sum(dpois(data, m, log =TRUE))
まず関数を定義します.Rで関数を定義するときはfunction(変数)の後にその内容を記述します.dpois(data,m,log=TRUE)では任意のパラメータmのポアソン分布において,dataを確率変数としたときの確率密度が出力されます.この際log=TRUEとしているので確率は対数で表されます.尤度は確率の積ですから,logにすると足し算となってsum()を使用することとなります.
lambda <- seq(2, 7, 0.1)
次にパラメータとなるlambdaを設定します.今回は大体4~5くらいで最大になりそうなので,2から7の間で0.1刻みの数を代入します.
plot(lambda, sapply(lambda, logL), type="l"
sapply()はある数列に対して,特定の関数を適用する関数です.ここではlambdaに格納されている数をlogLの変数に代入した結果をy軸に,lambdaをx軸にプロットした図が出力されます.
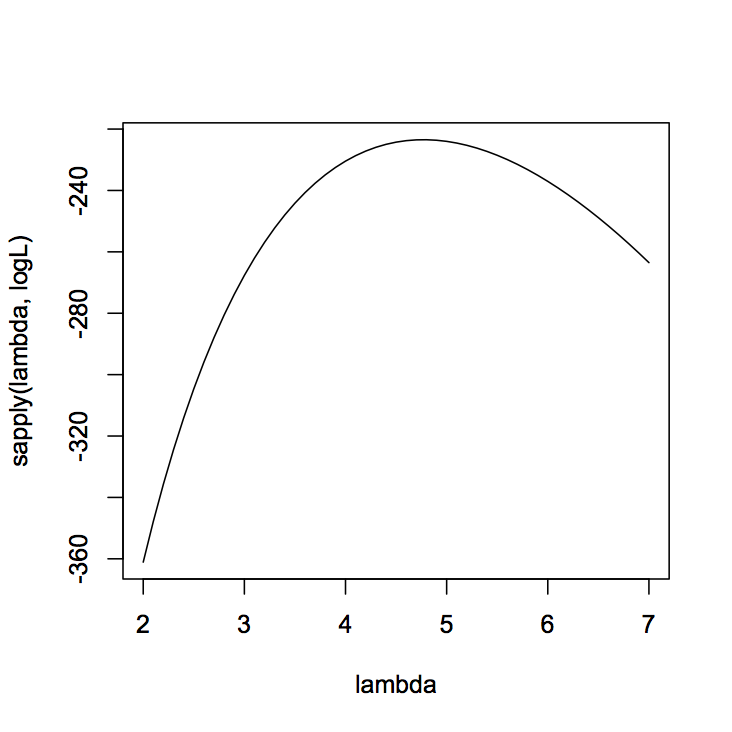
さて,このときの最尤推定値はこのグラフの傾きが0となるところですから,対数尤度関数を偏微分してイコールゼロとなるときのlambdaを求めるわけですが,この辺はみどり本通りにデータの標本平均となり,4.77となります.
大体こんな感じでしょうか.やっと一歩踏み出した感じですが,引き続き頑張ります.